
问题1:有界函数的界是否唯一?查看答案
∣f(x)∣≤M < M +1
按照定义,M +1显然也是函数f(x)的一个界.依此类推,可知任意大于M的正数都是函数f(x)的界.
问题2:周期函数的周期是否唯一?查看答案

是否存在无穷多个数域?
思路详解:

下面把在中学里大家已经知道的函数的基本属性复习一下,也就是:函数的单调性、奇偶性、有界性、周期性.
当一个变量增加时另一个变量也跟着增加,这样的函数就叫做单调增加的函数.从图形上看这条曲线,曲线上的点x在增加的时候,它所对应的纵坐标y也在增加,这样的函数是单调增加的.单调减少是相反的,随着x的增加相对应的y在减少,这样的函数是单调减少的,正如图形中演示的这样.如果函数当x在增加的时候,它所对应的y不是增加,也不是减少,这样的函数就不具有单调性.
一个函数的图形如果关于y轴对称,这样的函数就称为偶函数.从图形上来分析,曲线上任一点关于y轴的对称点也在曲线上面,这条曲线所描绘的函数就是偶函数.从解析式上看,如果有
f(-x)=-f(x)
f(x)就叫做偶函数.
一个函数的图形如果关于原点对称,这样的函数就称为奇函数.曲线上任一点关于原点的对称点也在曲线上面,这条曲线所描绘的函数就是奇函数.从解析式上看,如果有
f(-x)=-f(x)
f(x)就叫做奇函数.
如果自变量在定义域中变化时,函数值始终在一个有限的区间内变化,如图形中演示的,无论怎样变化,都有
-M ≤ f(x) ≤ M
这条曲线所反映的函数就是有界函数.
如果存在一个正数T,对任意的自变量x,有
f(x + T )=f(x)
这样的函数就叫做周期函数.从图形上反映,这个函数在相隔为T的任意两点上函数值都是一样的.也可以这样来看,从任意一点出发,以长度T为间隔划分区间,在每个区间上的函数图形都是可以完全重合的.
 现更换成一台新仪器,已知其测定的尺寸,方差不变仍是0.0022,现要检查其测定尺寸的均值是否有变化?(α=0.01)
现更换成一台新仪器,已知其测定的尺寸,方差不变仍是0.0022,现要检查其测定尺寸的均值是否有变化?(α=0.01)现利用新仪器测定了10个元件,结果为(单位:cm)
3.281 3.276 3.278 3.286 3.279
3.278 3.281 3.279 3.280 3.277
解:假设μ=3.278
由
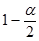 =0.995,查表得出
=0.995,查表得出 =2.575
=2.575接受域为[-2.575,2.575]
样本均值
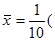 3.281+3.276+3.278+3.286+3.279
3.281+3.276+3.278+3.286+3.279+3.2789+3.281+3.279+3.280+3.277)
=3.2795
计算统计量值
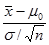 =
=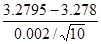 =2.37
=2.37因为2.37∈[-2.575,2.575],所以接受μ=3.278的假设,或说μ和3.278无显著差异.
若取α=0.05,则
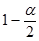 =0.975,查表得出
=0.975,查表得出 =1.96,所以接受域为[-1.96,1.96].
=1.96,所以接受域为[-1.96,1.96].因为2.37
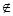 [-1.96,1.96],所以拒绝假设μ=3.278的假设,或说μ和3.278有显著差异.
[-1.96,1.96],所以拒绝假设μ=3.278的假设,或说μ和3.278有显著差异.(1)
答案:
1. (1)在![]() 单调减少.;(2)在
单调减少.;(2)在![]() 单调减少,在
单调减少,在![]() 单调增加.
单调增加.
2. (1)奇函数;(2)奇函数;(3)偶函数
