(1)y= ln(x+
(2)y= xsin x;
(3)y= x5+2
解:(1)因为 f (-x)= ln((-x)+
利用无理式的共轭及对数性质化简。
f (-x)=ln((-x)+ =ln(
=ln(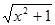 -x)
-x)
=ln[ ]=ln[
]=ln[ ]
]
=ln[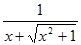 ]=-ln(x+
]=-ln(x+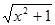 )
)
=ln[
=ln[
利用定义1.3,再利用关于奇偶函数的几个结论。
所以 f(-x)与-f(x)_________,因此,函数y=ln(x+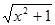
_______________________。
_______________________。
利用奇偶函数定义。
因为f (-x) =-ln(x+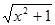 )=-f (x), 所以由奇偶函数定义可知,y=ln(x+
)=-f (x), 所以由奇偶函数定义可知,y=ln(x+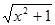 )是奇函数。
)是奇函数。
A) 相等,奇函数
(2)数y=xsin x是_____________________
利用关于奇偶函数的几个结论。
因为y=x和 y=sin x 都是奇函数,而奇函数和奇函数的乘积是偶函数,所以y=xsin x 是偶函数
。
A) 偶函数
(3)数y=x5+2是_____________________________________
找出不满足奇偶函数定义的点。
取 x=1,-1,f (1)=3,f (-1)=1,显然
f (1) ≠-f (-1)
由此可知y=x5+2 不是奇函数.又显然
f (1) ≠f (-1)
由此可知y=x5+2 不是偶函数.
C) 既不是奇函数也不是偶函数