假设检验是与点估计、区间估计有区别的另一类问题.
点估计面临的问题是：总体里含有未知参数，解决的方法是根据样本求出 一个量去代替未知参数；区间估计面临的问题也是总体里含有未知参数，解决的方法是确定一个区间以一定的概率去覆盖未知参数；而假设检验面临的问题更加广泛，可以推断总体里含有的未知参数，总体服从什么分布，甚至两个总体的期望或方差是否相同.例如到达港口的船只数量服从什么分布？解决的思路是假设这个分布是服从泊松分布，那么是否可以接受这种假设呢？下面看引例.
例　某种产品按规定次品率不超过4%才能出厂,今从一批产品中抽查10件,发现有4件次品,问这批产品能否出厂?
解　假设次品率等于4％
P(任抽10件发现4件次品)＝

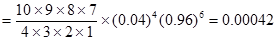
这说明，在假设成立的条件下，发生抽样这种结果的概率是很小的.这种事件称为小概率事件.
实际生活中，大家能够接受这样一个原理——小概率事件原理：小概率事件在一次抽样中是不会发生的”,而该问题使得小概率事件发生,说明假设是不对的,从而拒绝假设,表明这批产品不能出厂.
假设检验的思想：
1．对所研究的总体作某个假设.(譬如:假设其未知的E(X)=90;假设其未知的D(X)=15;假设两个总体的E(X)=E(Y);假设X的分布是正态分布，等等.)
2．通过抽样的样本值来检验是否接受假设?
是否接受的标准就是看在假设成立条件下发生抽样结果的事件是否为小概率事件?若是，就拒绝假设；否则就接受假设.
用假设检验来做判断,有可能是错误的,两类错误都有可能,即把真说成假或把假说成真.为了减少错误可以通过调节“小概率事件”的标准(p＜α),一般取α=0.10,0.05,0.01，称α为检验的显著性水平，或者和区间估计中一样，称为置信度. 取得越小,拒绝假设的可能越小,即将真说成假的错误就会减少,但将假说成真的错误就会增加.如果要同时减少这两类错误,则可采取增加样本容量的办法.
单正态总体均值的检验
已知方差σ²的情形(U检验)
问题:已知总体,其中σ²已知,现要通过抽样检测判断μ=μ₀?
第一步 假设μ=μ₀
第二步 适当选取一个样本的统计量，在已知σ²的条件下,选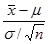
因在假设μ=μ₀的条件下:
第三步 根据显著性水平α,确定拒绝域和接受域.
由标准正态分布数值表,查出满足下述关系的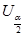

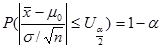
由概率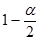查表得出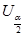，于是接受域为[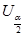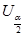－，]，拒绝域为(-∞, 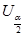－)或(,+∞)；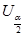
第四步 计算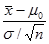，视其属于什么区域而作出判断.