导线内业计算包括角度闭合差的计算和调整、方位角的推算、坐标增量闭合差的计算和调整及未知点的坐标计算。
1、角度闭合差的计算和调整
1）角度闭合差计算：
a)附合导线 ：
CD的方位角推算值
与其已知值
若不等，其差值即称为角度闭合差
。 
= 
－
＝
－(
－
) 
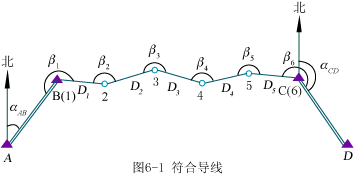
(6-3)b)闭合导线
闭合导线角度闭合差为所有内角观测值之和与闭合
边形内角和理论值
之差，即 
－
(6-8)2）角度闭合差的调整
如果
小于限差，说明观测成果符合要求，但是需要调整。即将角度闭合差按相反符号平均分配于各角(其分配值即称原角度观测值之改正数)。 注：分配值一般取整至秒，并使其总和与角度闭合差二者绝对值相等。
3) 根据改正后的角值，重新计算各边的坐标方位角。
根据改正后的角值，重新计算各边的坐标方位角。、最后算得的
和已知值
应完全相等，可作为检核。 
＝
＋
＝
－
注：上二式右端，若前两项计算结果<
，
前面用“＋”号，否则
前面用“－”号。2、坐标增量闭合差的计算合调整
1）坐标闭合差计算
坐标增量闭合差是末端已知点坐标的计算值
、
和已知值
、
之差(分别称为纵坐标增量闭合差
和横坐标增量闭合差
)： a）附合导线
(6-4a)
(6-4b)b)闭合导线
闭合导线的起、终点为同一点，故将公式(6-4)式右端之第2项均改为0，即为闭合导线坐标增量闭合差。
2）闭合差调整
a）根据
、
计算导线全长闭合差
和全长相对闭合差K： 
(6-5)
(6-6)如果
小于限差，说明观测成果符合要求，但亦需要调整。 b）将纵、横坐标增量闭合差
、
反号，按与边长成比例分配于各边的坐标增量中 其分配值(即原纵、横坐标增量值之改正数)
、
按下式计算： 
式中，
为第
条边边长。 注：纵、横坐标增量改正数之的总和应分别等于纵、横坐标增量闭合差，而符号相反，用于检核。
3) 计算待定导线点坐标
坐标增量闭合差调整后，根据起始点的已知坐标和经改正后的坐标增量计算各待定导线点的坐标。
注：最后算得的末端点
、
坐标应和其已知值完全相符合，再次检核。二、举例
例1 已知四边形闭合导线内角的观测值见下表，试进行角度闭合差计算和调整，并推算出各边的坐标方位角。
|
|||||||||||||||||||||||||||||||||||
∑βi=360°00′20″
－
=20″ （n＝4） 
120″ fβ＜fβ允 ，精度符合要求。
2）调整角度闭合差
将角度闭合差按相反符号平均分配于各角：－20″/4＝－5″。
计算改正后角值各内角值βi′＝βi＋（－5″）
3）推算各边方位角
因角度观测值为右角，故应用公式
＝
－
推算各边方位角。计算时应注意公式右端，若前两项计算结果<
，
前面用“＋”号，否则
前面用“－”号。已知 α12＝100°00′00″
故 α23＝α12＋β2′＝100°00′00″－67°14′07″＋180°＝212°45′53″
α34＝α23＋β3′＝212°45′53″－54°15′15″＋180°＝158°30′38″
α41＝α34＋β4′＝158°30′38″－126°15′20″＋180°＝212°15′18″
α12＝α41＋β1′＝212°15′18″－112°15′18″＋180°＝100°00′00″
α12推算结果与已知值α12＝100°00′00″相同，说明计算无误。
如下所示，计算成果填入表中。
|
|||||||||||||||||||||||||||||||||||
－
=20″ 
120″  |
