对精度要求较高的钢尺量距，除应采用经纬仪定线、在钢尺的尺头处用弹簧秤控制拉力等措施而外，还应对丈量结果进行以下三项改正：
1、尺长改正
设钢尺名义长为
，在一定温度和拉力条件下检定得到的实际长为
，二者之差值即为一尺段的尺长改正
： 
(4-5) 2、温度改正
受热胀冷缩的影响，当现场作业时的温度
与检定时的温度
不同时，钢尺的长度就会发生变化，因而每尺段需进行温度改正
： 
(4-6)式中
C，为钢尺的膨胀系数。 3、倾斜改正
设一尺段两端的高差为
，沿地面量得斜距为
，将其化为平距
(图4-6)，应加倾斜改正
。 因为
， 即有
＝
；又因
甚小，可近似认为
，所以有
＝－
(4-8)以上三项之和即为一尺段的改正数
： 
(4-9)4、尺长方程式
尺长随温度变化的函数式称为尺长方程式：
(4-7)式中
―温度为
度时钢尺的实际长度；
―钢尺的名义长度；等式右端后两项实际上就是钢尺尺长改正和温度改正的组合。 5、相对误差
为了检核和提高精度，一般需要进行往返丈量，取其平均值作为量距的成果。
(4-3) 并以往、返丈量结果的相对误差来衡量其成果的精度。
相对误差：
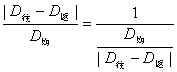(4-4)
二、举例
例1：钢尺丈量AB的水平距离，往测为375.31m，返测为375.43m；丈量CD的水平距离，往测为263.37m，返测为263.47m，最后得DAB、DCD及它们的相对误差各为多少 哪段丈量的结果比较精确
解：1)水平距离，由 
得：
AB： DAB＝（375.31＋375.43）/2＝375.37m
CD： DCD＝（263.37＋263.47）/2＝263.42m
2)相对误差，由
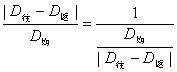得：
AB：KAB＝(375.43－375.31)/375.37＝1/3128
CD：KCD＝(263.47－263.37)/263.42＝1/2634
KAB＜KCD，故AB的丈量结果比较精确。
例2：一钢尺名义长
=30m，实际长
=30.0025m，检定温度
＝
C，作业时的温度和场地坡度变化都不大，平均温度
＝
C，尺段两端高差的平均值
＝+0.272m，量得某段距离往测长
＝221.756m，返测长
＝221.704m，求其改正后平均长度及其相对误差。
解：一尺段尺长改正 
＝30.0025-30.000=+0.0025m
温度改正 
=0.0000125
=0.0022m
倾斜改正 
=－
=－0.0012m
三项改正之和 
= 0.0025+0.0022－0.0012＝+0.0035m
往测长
的改正数及往测长
=
=+0.026m，
m
返测长
的改正数及返测长
=+0.026m，
m
改正后平均长：
＝221.756m
相对误差：
例3：从A点测设长度为140.685m的水平距离AB，初设B点后，测得温度t=23℃,AB两点的高差h=－1.168m，已知尺长方程为lt=30－0.0023+1.2×10-5(t－20°C)×30m,问需沿地面测设多少长度
解：1）AB段三项改正
尺长改正 
＝－0.0023×140.685/30＝－0.0108m
温度改正 
＝1.2×10-5(23°C－20°C)×140.685＝0.0051m
倾斜改正 
＝－1.1682/(2×140.685)＝－0.0048m
三项之和（即AB段的改正数）：
＝－0.0108＋0.0051＋（－0.0048）
＝－0.0101m
需沿地面测设的长度 DAB′＝DAB－
＝140.685－(－0.0101)＝140.786m
 |
