学习目标
本节课学习目标:通过本节课学习,了解边际成本、边际收入、边际利润的概念,会求成本、收入、利润等经济函数的边际值和边际函数.
一企业的每日成本 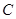 (千元)是日产量
(千元)是日产量 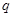 (台)的函数
(台)的函数
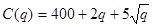 求:(1)当产量为400台时的成本;
求:(1)当产量为400台时的成本;
(2)当产量为400台时的平均成本;
(3)当产量由400台增加到484台时的平均成本;
(4)当产量为400台时的边际成本.
解:(1)当产量为400台时的成本为:
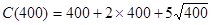 =1 300(千元)
=1 300(千元)
(2)当产量为400台时的平均成本为:
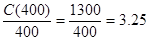 (千元/台)
(千元/台)
(3)当产量由400台增加到484台时的平均成本:
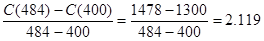 (千元/台)
(千元/台)
(4)当产量为400台时的边际成本为:
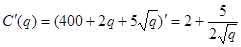
所以, (千元/台)
(千元/台)
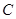 (千元)是日产量
(千元)是日产量 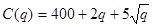
(2)当产量为400台时的平均成本;
(3)当产量由400台增加到484台时的平均成本;
(4)当产量为400台时的边际成本.
解:(1)当产量为400台时的成本为:
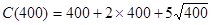 =1 300(千元)
=1 300(千元)(2)当产量为400台时的平均成本为:
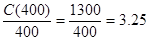 (千元/台)
(千元/台)(3)当产量由400台增加到484台时的平均成本:
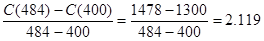 (千元/台)
(千元/台)(4)当产量为400台时的边际成本为:
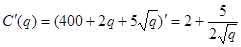
所以,
 (千元/台)
(千元/台)
某产品的销售量 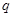 与单位价格
与单位价格 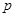 之间的关系为
之间的关系为
 求:(1)写出收入函数R与q之间的关系;
求:(1)写出收入函数R与q之间的关系;
(2)计算销售量达到300时的收入;
(3)销售量由300增加至360时,收入增加了多少?
(4)在这个过程中平均多销售一单位时,收入增加多少?
(5)求销售量为300时的边际收入.
解:(1) 收入函数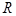 与 q 之间的关系为:
与 q 之间的关系为:
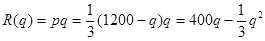
(2) 销售量达到300时,收入为:
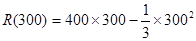 =90 000
=90 000
(3) 销售量由300增加至360时,收入增加了:
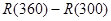 =100 800-90 000
=100 800-90 000
(4)在这个过程中平均多销售一单位时,收入将增加:
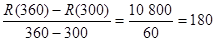
(5)因为
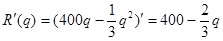
所以,销售量为300时,边际收入为:
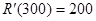

(2)计算销售量达到300时的收入;
(3)销售量由300增加至360时,收入增加了多少?
(4)在这个过程中平均多销售一单位时,收入增加多少?
(5)求销售量为300时的边际收入.
解:(1) 收入函数
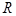 与 q 之间的关系为:
与 q 之间的关系为: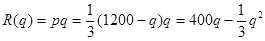
(2) 销售量达到300时,收入为:
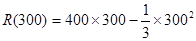 =90 000
=90 000(3) 销售量由300增加至360时,收入增加了:
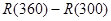 =100 800-90 000
=100 800-90 000(4)在这个过程中平均多销售一单位时,收入将增加:
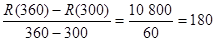
(5)因为
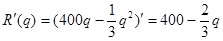
所以,销售量为300时,边际收入为:
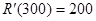
某企业每天的产量均能售出,售价为490元/吨,其每日成本 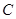 与每日产量
与每日产量 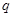 之间的函数为
之间的函数为
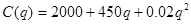 求:(1)写出收入函数;
求:(1)写出收入函数;
(2)写出利润函数;
(3)求利润函数的导数,并说明其经济意义.
解:(1) 收入函数为:
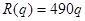
(2) 利润函数为:
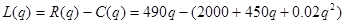
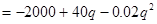
(3) 利润函数的导数为:
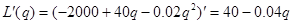
利润函数的导数称为边际利润,其经济意义为:当产量达到q时,再增加单位产量后利润的改变量.
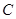 与每日产量
与每日产量 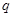 之间的函数为
之间的函数为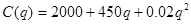
(2)写出利润函数;
(3)求利润函数的导数,并说明其经济意义.
解:(1) 收入函数为:
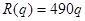
(2) 利润函数为:
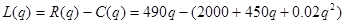
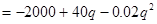
(3) 利润函数的导数为:
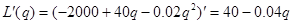
利润函数的导数称为边际利润,其经济意义为:当产量达到q时,再增加单位产量后利润的改变量.
某厂每月生产 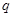 (百件)产品的总成本为
(百件)产品的总成本为  (千元). 若每百件的销售价格为4万元,试写出利润函数
(千元). 若每百件的销售价格为4万元,试写出利润函数 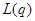 ,并求当边际利润为0时的月产量.
,并求当边际利润为0时的月产量.
解:已知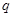 (百件),
(百件),  (千元),
(千元), 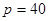 (千元/百件)
(千元/百件)
(1)利润函数为:
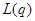 =
=
(2)边际利润为
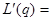 40 - (2q -2
40 - (2q -2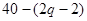
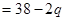
令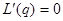 ,即
,即
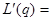
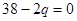
得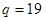
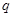 (百件)产品的总成本为
(百件)产品的总成本为  (千元). 若每百件的销售价格为4万元,试写出利润函数
(千元). 若每百件的销售价格为4万元,试写出利润函数 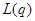 ,并求当边际利润为0时的月产量.
,并求当边际利润为0时的月产量.解:已知
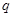 (百件),
(百件),  (千元),
(千元), 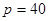 (千元/百件)
(千元/百件)(1)利润函数为:
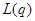 =
=
(2)边际利润为
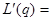 40 - (2q -2
40 - (2q -2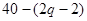
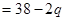
令
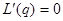 ,即
,即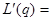
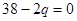
得
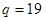
1. 某工厂每日产品总成本 C(百元)与日产量 q(kg)的关系为
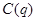 = 4
= 4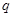 +
+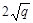 +500
求日产量为900 kg时的边际成本.
+500
求日产量为900 kg时的边际成本.
2. 某厂每月生产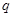 (百件)产品的总成本为
(百件)产品的总成本为  (千元).若每百件的销售价格为4万元,试写出利润函数
(千元).若每百件的销售价格为4万元,试写出利润函数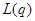 ,并求当边际利润为0时的月产量.
,并求当边际利润为0时的月产量.
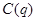 = 4
= 4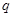 +
+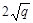 +500
+5002. 某厂每月生产
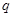 (百件)产品的总成本为
(百件)产品的总成本为  (千元).若每百件的销售价格为4万元,试写出利润函数
(千元).若每百件的销售价格为4万元,试写出利润函数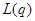 ,并求当边际利润为0时的月产量.
,并求当边际利润为0时的月产量.
答案:
1. 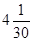 百元/kg.
百元/kg.
2. 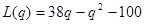 ,
, 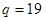 百件
百件


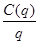 — —平均成本函数
— —平均成本函数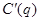 — —产量为 时的边际成本函数
— —产量为 时的边际成本函数