1.应用条件:结点无未知线位移的刚架与连续梁。
2.正负号规定:杆端弯矩以顺时针为正。相应地,结点力偶荷载及转动约束中的约束力矩均以顺时针为正。
3.基本参数
⑴转动刚度S:使杆端发生单位转角(其他杆端位移分量为零)时,需在该端(即近端)施加的杆端力矩。转动刚度的大小与线刚度及远端支承情况有关。
⑵力矩分配系数μ:杆Aj在结点A的力矩分配系数μAj,等于该杆A端转动刚度SAj与交于结点A的各杆转动刚度之和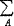 S的比值,即 S的比值,即
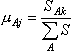
⑶传送系数C:当杆Aj近端有转角时,远端弯矩与近端弯矩的比值,即
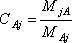
传递系数大小与杆件远端支承情况有关。
等截面杆的转动刚度与传递系数(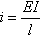 )
)
远端支承 |
转动刚度 |
传递系数 |
远端固定
远端铰结
远端滑动
远端自由 |
S=4i
S=3i
S=i
S=0 |
C=1/2
C=0
C=-1
C=0 |
|
4.单结点的力矩分配
⑴单结点连续梁或刚架仅有结点力偶荷载M0作用时,将力偶M0乘以各杆的力矩分配系数,即得各杆近端弯矩
MAj= μAj M0
M0以顺时针为正,所得各杆近端弯矩也为正值;M0若为逆时针,则MAj为负值,可称为“同号分配”。
此时在杆远端弯矩为
MjA= CAj MAj
当结点D作用有力偶荷载M时,结点D上各杆件近端得到按各杆的分配系数乘以M的近端弯矩,也称分配弯矩;各杆的远端则有传递系数乘以近端弯矩的远端弯矩,也称传递弯矩(见动画)。
⑵杆上有跨间荷载作用时,单结点连续梁(左图(a))或刚架的计算分为三步:
第一步,加转动约束锁紧钢结点A(左图(b)),求出各单杆的固端弯矩MF。结点处各杆固端弯矩之和即为约束力矩MA。
第二步,撤除转动约束放松结点A,相当于在结点A加力偶(- MA)。在此力偶作用下求各杆近端分配力矩和远端传递力矩(左图?)。
第三步,叠加以上两步计算所得杆端弯矩,就得到原结构的杆端弯矩。
以上过程可归结为“先锁、后松,再叠加”。
5.多结点的力矩分配
多结点连续梁或刚架计算,是以单结点力矩分配为基本环节的渐近计算,其步骤如下:
⑴先锁:加约束锁紧全部刚结点,计算各杆的固端弯矩和结点的约束力矩。约束力矩MA =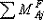 。
。
⑵逐次放松:每次放松一个结点(邻近结点仍锁住)进行单结点的力矩分配与传递。轮流放松各结点,经多次循环后各结点渐趋平衡。实际计算一般进行2~3个循环就可获得足够精确度。
⑶叠加:将各次计算所得杆端弯矩相加(代数和)就得到杆端弯矩,即
M = MF+ΣM分配+ΣM传递
计算格式见例题。 |